numpy.polynomial.chebyshev.chebfromroots
-
numpy.polynomial.chebyshev.chebfromroots(roots)[source] -
Generate a Chebyshev series with given roots.
The function returns the coefficients of the polynomial
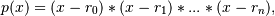
in Chebyshev form, where the
r_nare the roots specified inroots. If a zero has multiplicity n, then it must appear inrootsn times. For instance, if 2 is a root of multiplicity three and 3 is a root of multiplicity 2, thenrootslooks something like [2, 2, 2, 3, 3]. The roots can appear in any order.If the returned coefficients are
c, then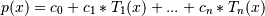
The coefficient of the last term is not generally 1 for monic polynomials in Chebyshev form.
Parameters: roots : array_like
Sequence containing the roots.
Returns: out : ndarray
1-D array of coefficients. If all roots are real then
outis a real array, if some of the roots are complex, thenoutis complex even if all the coefficients in the result are real (see Examples below).See also
polyfromroots,legfromroots,lagfromroots,hermfromroots,hermefromroots.Examples
>>> import numpy.polynomial.chebyshev as C >>> C.chebfromroots((-1,0,1)) # x^3 - x relative to the standard basis array([ 0. , -0.25, 0. , 0.25]) >>> j = complex(0,1) >>> C.chebfromroots((-j,j)) # x^2 + 1 relative to the standard basis array([ 1.5+0.j, 0.0+0.j, 0.5+0.j])
© 2008–2016 NumPy Developers
Licensed under the NumPy License.
https://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.polynomial.chebyshev.chebfromroots.html