numpy.linalg.cholesky
-
numpy.linalg.cholesky(a)[source] -
Cholesky decomposition.
Return the Cholesky decomposition,
L * L.H, of the square matrixa, whereLis lower-triangular and .H is the conjugate transpose operator (which is the ordinary transpose ifais real-valued).amust be Hermitian (symmetric if real-valued) and positive-definite. OnlyLis actually returned.Parameters: a : (..., M, M) array_like
Hermitian (symmetric if all elements are real), positive-definite input matrix.
Returns: L : (..., M, M) array_like
Upper or lower-triangular Cholesky factor of
a. Returns a matrix object ifais a matrix object.Raises: LinAlgError
If the decomposition fails, for example, if
ais not positive-definite.Notes
New in version 1.8.0.
Broadcasting rules apply, see the
numpy.linalgdocumentation for details.The Cholesky decomposition is often used as a fast way of solving
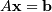
(when
Ais both Hermitian/symmetric and positive-definite).First, we solve for
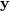 in
in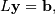
and then for
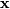 in
in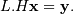
Examples
>>> A = np.array([[1,-2j],[2j,5]]) >>> A array([[ 1.+0.j, 0.-2.j], [ 0.+2.j, 5.+0.j]]) >>> L = np.linalg.cholesky(A) >>> L array([[ 1.+0.j, 0.+0.j], [ 0.+2.j, 1.+0.j]]) >>> np.dot(L, L.T.conj()) # verify that L * L.H = A array([[ 1.+0.j, 0.-2.j], [ 0.+2.j, 5.+0.j]]) >>> A = [[1,-2j],[2j,5]] # what happens if A is only array_like? >>> np.linalg.cholesky(A) # an ndarray object is returned array([[ 1.+0.j, 0.+0.j], [ 0.+2.j, 1.+0.j]]) >>> # But a matrix object is returned if A is a matrix object >>> LA.cholesky(np.matrix(A)) matrix([[ 1.+0.j, 0.+0.j], [ 0.+2.j, 1.+0.j]])
© 2008–2016 NumPy Developers
Licensed under the NumPy License.
https://docs.scipy.org/doc/numpy-1.11.0/reference/generated/numpy.linalg.cholesky.html