numpy.polyint

numpy.polyint(p, m=1, k=None) [source]

Return an antiderivative (indefinite integral) of a polynomial.

The returned order m antiderivative P of polynomial p satisfies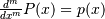 and is defined up to m - 1 integration constants k. The constants determine the low-order polynomial part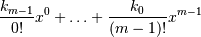

of P so that .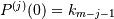

Parameters:

p : array_like or poly1d Polynomial to differentiate. A sequence is interpreted as polynomial coefficients, see poly1d. m : int, optional Order of the antiderivative. (Default: 1) k : list of m scalars or scalar, optional Integration constants. They are given in the order of integration: those corresponding to highest-order terms come first. If None (default), all constants are assumed to be zero. If m = 1, a single scalar can be given instead of a list.

See also

polyder

derivative of a polynomial

poly1d.integ

equivalent method

Examples

The defining property of the antiderivative:

>>> p = np.poly1d([1,1,1])
>>> P = np.polyint(p)
>>> P
poly1d([ 0.33333333,  0.5       ,  1.        ,  0.        ])
>>> np.polyder(P) == p
True

The integration constants default to zero, but can be specified:

>>> P = np.polyint(p, 3)
>>> P(0)
0.0
>>> np.polyder(P)(0)
0.0
>>> np.polyder(P, 2)(0)
0.0
>>> P = np.polyint(p, 3, k=[6,5,3])
>>> P
poly1d([ 0.01666667,  0.04166667,  0.16666667,  3. ,  5. ,  3. ])

Note that 3 = 6 / 2!, and that the constants are given in the order of integrations. Constant of the highest-order polynomial term comes first:

>>> np.polyder(P, 2)(0)
6.0
>>> np.polyder(P, 1)(0)
5.0
>>> P(0)
3.0